Spacecraft rendezvous problem

Mar 15, 2019 2 min read

High-level description

We wish to drive a spacecraft (Deputy) towards another spacecraft (Chief) for docking. This problem is known as the spacecraft rendezvous and docking problem. It is a common requirement for maintenance and resupply missions in space applications. Due to sensing constraints, we wish that the Deputy stays within a line-of-sight cone with respect to Chief. Further, we wish to achieve the docking in a pre-specified time interval while obeying the physical laws that govern the system and constraints on actuation (limited thrust).

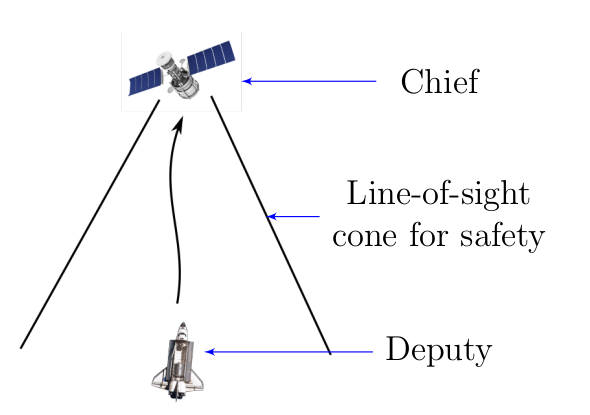
Satellite rendezvous and docking problem

We model the Deputy satellite dynamics in the relative coordinate frame of the Chief. Loosely, we have the following constraints we wish to satisfy apart from the dynamics and control constraints,

  1. Reach constraint: Reaching a target set centered at the origin. This set can encode relative velocity constraints (should dock slowly) and tolerances in relative position at the time of rendezvous.
  2. Avoid constraint: We wish to stay within a safe set, given by a stationary cone (line-of-sight cone) with the tip at the origin.

Formal specification

Drive the Deputy satellite such that it

  1. reaches the target set at a pre-specified time,
  2. stays within the safe set (staying out of the avoid set) during the time interval,
  3. satisfies the dynamics constraints, and
  4. satisfies the control constraints.

Safety problem

Identify the set of initial states and synthesize an admissible controller that achieves the given specification with a probability above a pre-specified likelihood threshold. Such initial states will be declared safe.

For safety-critical applications, it is important that we construct either exact or underapproximations of the set of safe initial states. We do not want to be over-confident in our safety declarations, i.e., declare an initial state safe when it is not really safe.

Results

SReachTools can address this question, and generate underapproximations of the set of safe initial states.

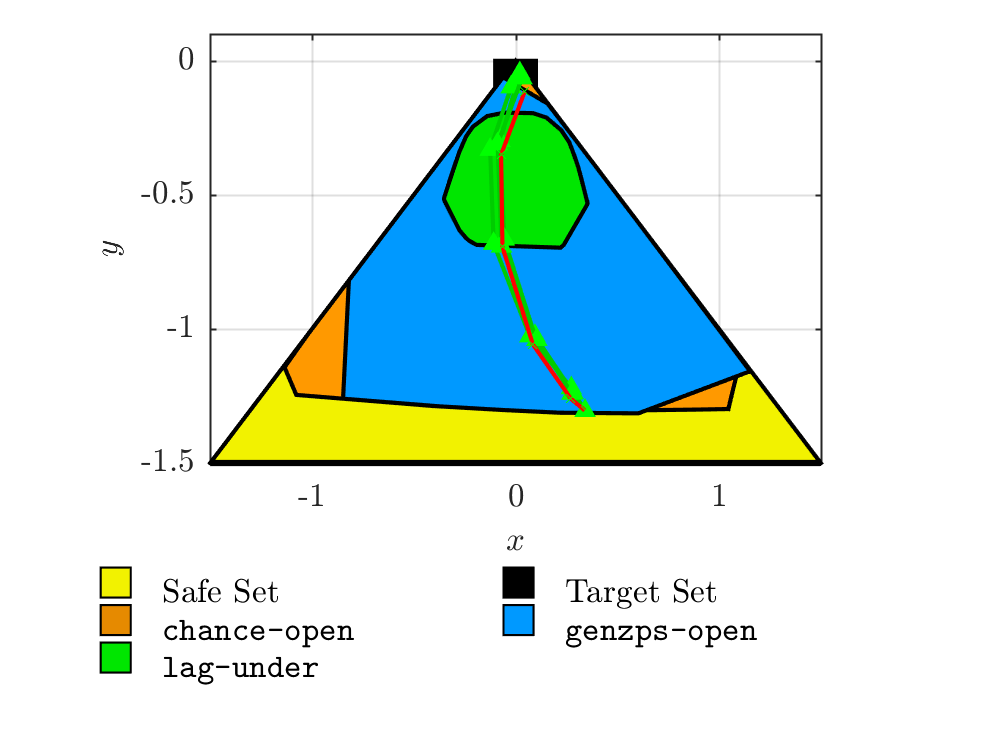
Various underapproximations of the set of initial locations with probability of satisfying the specification greater than 0.8. A Monte-Carlo simulation of the resulting trajectory from one of the safe initial states is also shown.

Figure 2 shows various underapproximations of the set of initial locations obtained using SReachTools. These are the safe initial states from which the Deputy can be driven to satisfy the specification with a likelihood no smaller than 0.8. A Monte-Carlo simulation of the safe trajectory is shown from one of the safe initial states under the synthesized controller. Out of 5 randomly chosen trajectories, only one fails (violates terminal velocity constraints).

stochastic-optimal-control
Research Scientist

Researcher with experience in optimization, control, stochastic modeling, and reinforcement learning