Safety under uncertainty and constraints
Automation, typically, refers to the use of an onboard computer to drives a system to optimize some objective. It makes our day-to-day life simpler and efficient, for example, in transportation ( autopilot systems and self-driving cars), space applications, biomedical applications, power grid, and the list goes on and on. However, as we hand over more and more control to the automation, we naturally seek guarantees of safety and performance. After all, we do not want to spend billions of dollar in R&D and develop an automation that may cause harm.
Why is providing safety guarantees in automated control systems for real-world problems hard?
In control theory, we attack real-world problems by formulating a mathematical model and studying its relevant properties. The two key challenges in providing the desired safety guarantees for real-world systems are stochasticity and high-dimensionality.
Stochasticity in our models help us capture human inputs (like actions of the other drivers on the street for the self-driving car problem), disturbance effects (like weather in air navigation/power grid systems), varying parameters (like patient parameters in biomedical devices), and other unmodelled phenomena. For example, we can describe the error between our simplified model and the more complicated true mathematical model via a stochastic error term.
High-dimensional systems evolve as a function of a larger set of states, and thereby allowing the mathematical model to be closer to the reality compared to their low-dimensional models.
How do we formally obtain a safety guarantee? Terminal stochastic reach-avoid problem
The following information is required:
- the stochastic system dynamics along with the bounded control space,
- the safe set, and
- the target set.
We wish to satisfy the following specification:
- Ensure that the system reaches the target set at a finite time horizon (not before). (Reach constraint)
- Ensure that the system stays within the safe set during the time interval. (Safety constraint)
We seek to address the following verification problem[^2]:
Identify the set of initial states and design an admissible controller that maximizes the probability of satisfaction of a specification.
Such a specification is called a terminal hitting-time stochastic reach-avoid problem. It is a special class of verification problems, which has been well studied for the past couple of decades in computer science as well as control theory. See this paper by Sean Summers and John Lygeros for more details.
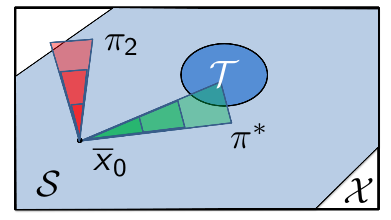
Stochastic reachability of a target tube: A general framework for safety
This problem can be generalized to a time-varying collection of safe sets. Motivated by the classical work of Bertsekas, we call this problem the stochastic reachability of a target tube. This problem is illustrated in Figure 2.
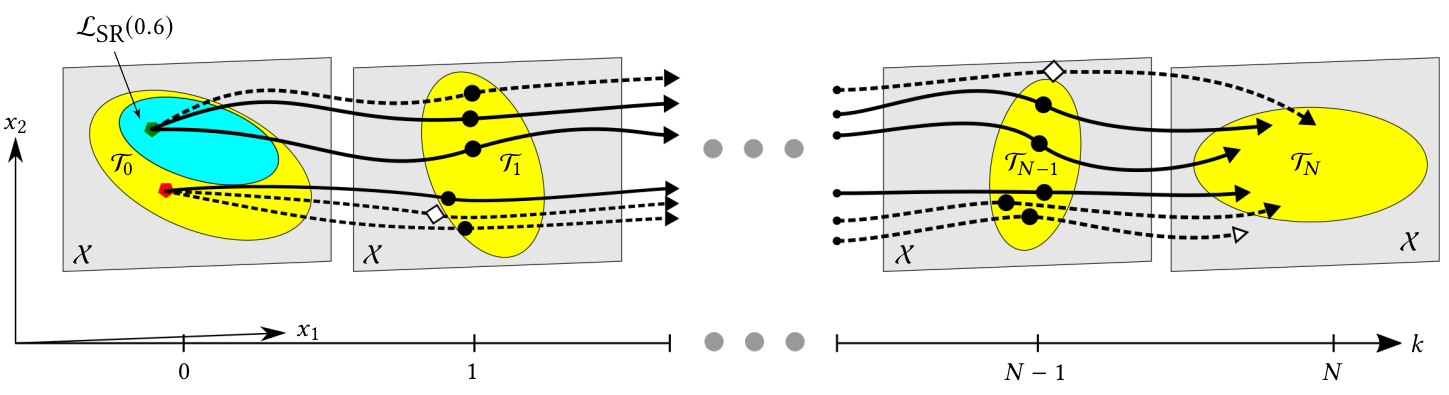
See my paper on stochastic reachability of a target tube for more details.
SReachTools
SReachTools is a user-friendly, open-sourced MATLAB toolbox that address these questions.
Applications
See the following posts for safety guarantees obtained for various applications: